Hace ya dos años, en una sesión de procrastinación incitada por el algoritmo de YouTube, me tropecé con un vídeo que me hizo especial gracia, cuyo título es exactamente el mismo que el de este post, pero en inglés. En el vídeo, un chico explicaba la forma correcta de cortar una pizza, la forma que un auténtico chad usaría, haciendo cortes verticales, en vez de radiales, pero asegurándose de que el área delimitada por cada uno sea la misma. Aunque nunca terminé de verlo, la idea se ha quedado grabada en mi backlog mental, así que vamos a explorarla.

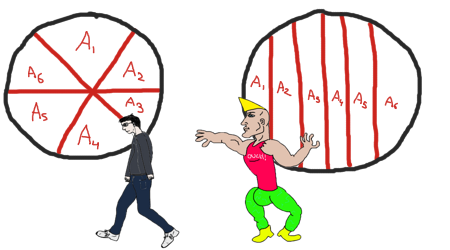
Primero, y a diferencia del vídeo, no voy a contemplar solo el caso de tres secciones (\(n=3\)), ni voy a limitar el radio de la pizza a siete pulgadas (\(r=7\)). Tampoco voy a hacer los cálculos sobre el cuarto de círculo, porque eso bifurca en dos el problema, dependiendo de si la cantidad de áreas es par o impar. Usaré directamente la mitad superior de la circunferencia, eliminando así la necesidad de considerar si existe un área central o no.

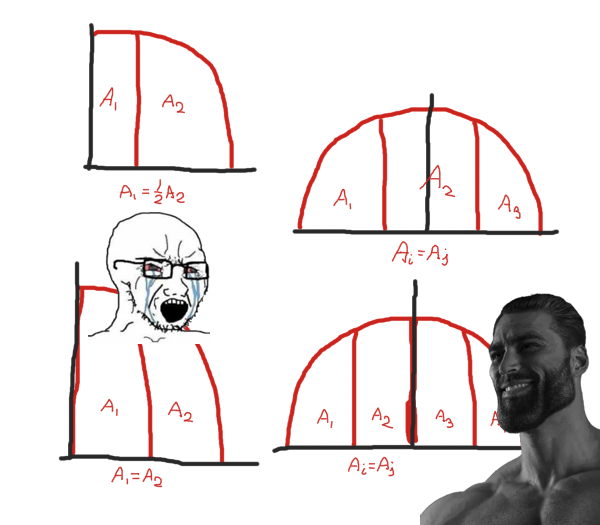
Dado que cada uno de los \(n\) pedazos ha de tener el mismo tamaño, sus áreas serán la \(n\)-ésima parte de la superficie total de la media pizza, \(A_i=\frac{1}{2n}\pi r^2\). Con esto podemos obtener el área acumulada al llegar al pedazo \(i\):

\begin{equation} \sum_{j=1}^i A_j = iA_i = \frac{i}{2n}\pi r^2 \end{equation}

Pero esa fórmula no nos es muy útil por sí misma porque, aunque calculásemos su resultado, todavía necesitaríamos saber por dónde hacer el corte. A esos valores de \(x\) los llamaremos \(a_i\), y serán la linde entre las áreas \(i\) e \(i+1\).

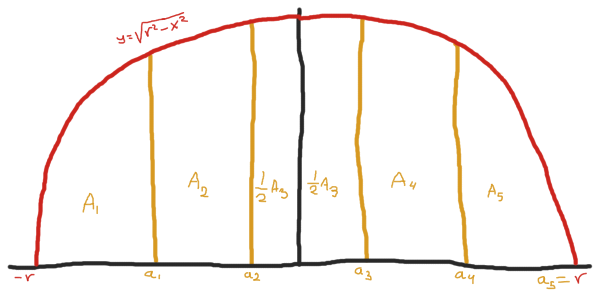
Dado que la fórmula de la media circunferencia es \(y=\sqrt{r^2-x^2}\), y que nuestra pizza teórica es un círculo perfecto, podemos obtener el área acumulada de los primeros \(i\)-pedazos de forma alternativa a la mostrada en la ecuación \((1)\), integrando la función entre \(-r\) y \(a_i\):

\begin{equation} \sum_{j=1}^i A_j = \int_{-r}^{a_i} \sqrt{r^2 - x^2} dx \end{equation}

Y ahora, juntando ambas definiciones de \(\sum_{j=1}^i A_j\) dadas en las ecuaciones \((1)\) y \((2)\), obtenemos la siguiente igualdad:

\begin{equation} \frac{i}{2n}\pi r^2 = \int_{-r}^{a_i} \sqrt{r^2 - x^2} dx \end{equation}

La cual puede ser resuelta, con un poco de cálculo, álgebra y Wolfram Alpha, a la siguiente expresión:

Por desgracia, es complicado despejar \(a_i\) de esta expresión, por lo que para calcular su valor en cada caso hay que emplear métodos numéricos, y eso es lo que vamos a hacer exactamente.

Simulando la ecuación

Abajo dejo un simulador que permite saber por dónde hacer los cortes en una pizza dados los parámetros \(r\) y \(n\). No es perfecto, y se podía optimizar bastante, por ejemplo entendiendo que cada punto de corte \(a_i\) estará entre otros dos, el anterior (\(a_{i - 1}\)) y \(r\), cerrando el rango de búsqueda de valores. También se podría aprovechar la simetría axial para reducir a la mitad los cálculos, pero creo que para un simulador de juguete ya sería pensarlo demasiado.

Yendo más allá

Si bien la solución dada más arriba es buena, lo cierto es que las pizzas nunca son perfectamente circulares. Una buena manera de aproximar la corteza de una pizza podría venir dada por la unión de dos funciones, \(f(x)\) para la \(y\geq0\) y \(-g(x)\) para \(y\leq0\) cuyos extremos se unan (El concepto de radio desaparecería en este caso):

Y después podríamos rehacer el procedimiento del post, cambiando la ecuación \((3)\) por:

También se podría calcular el área con una función polar \(\int_0^{2\pi} p(\theta)d\theta\) que respete \(p(0)=p(2\pi)\), que sería mucho más próxima a la realidad, pero que haría imposible aplicar el método que he seguido aquí.

De todas formas, ambos casos seguirían siendo imperfectos, porque hay pizzas con protuberancias asimétricas que impiden su representación como funciones, así que quizá habría que recurrir a alguna integral de línea cerrada \(\oint_C f(s)ds\) (donde \(C\) sea el contorno de la corteza), y no sé como atacar este problema.

Otra área de estudio abierta es la que aborda el famoso “Problema de la Corteza”, es decir, la necesidad de que cada pedazo de pizza contenga la misma cantidad de corteza que los demás. Esto es resuelto por cortes radiales convencionales, pero hay más formas de hacerlo, así que estaría bien describirlas en detalle.

Y nada, a ver si como pizza pronto, que tengo antojo.